Harmonic Series (Music)
The scale of nature
Definition
The harmonic series is the chord of partials that vibrate simultaneously when a natural tone is played.
Inhalt
- 1 Harmonic Series – Sound Sample
- 2 Chord of Harmonics
- 3 Timbre
- 4 Harmonic Series – Intervals
- 5 Harmonic Series – Frequency Ratios
- 6 Musicians and Physicists
- 7 Converting Frequencies into Pitches
- 8 Overtones vs Harmonics
- 9 Natural Tone Series vs. Harmonic Series
- 10 Examples: Harmonic series of F and E
- 11 Table of Harmonics
- 12 What are Overtones?
- 13 Glossary of Terms
- 14 Bibliography & Sources
- 15 Picture Credits
- 16 Tell a Friend
The harmonic series is the foundation of all musical scales and tuning systems, because it is the only natural scale. As soon as a tone sounds, overtones resonate. They all sound at the same time. The overtone series is therefore actually a chord. The structure is always the same and corresponds to a mathematical harmonic series, hence the name series. You don’t usually hear the overtones. Because they all vibrate as a chord at the same time, they seem to us like a single note.
The term overtone series refers to the harmonic partials (comparison of overtone/partial tone/harmonic, see below). There are also sounds with inharmonic overtones. The more inharmonic overtones there are in a sound, the more it becomes noisy.
The harmonics of A.
Harmonic Series of A2 (110 Hz).
All sounds consist of overtone chords. Only sine waves have no overtones. One sound differs from the other mainly in the volume of the individual overtones (besides the noise components and temporal sound changes). The overtone series is not only the basis for music. It enables us to speak and sing, recognize people by their voice, locate sounds and distinguish a piano from a flute.
This scale does not come from humans, but originates directly from the laws of vibration of nature. It follows a universal wave principle and we are able to hear and experience it. The tones differ from our usual equal tempered tone system. Nevertheless, the equal tempered system, like all other tuning systems, is derived from the overtone series.
The reason is that we assemble sequences of notes internally into small chords and then compare them unconsciously with the harmonic series. We have invented sound systems based on natural intervals because we love consonances with the harmonic series. However, cultures do not always consider the same intervals to be beautiful. Hence, there exist more than 4000 different sound systems in the world.
Our western system with 12 semitones per octave, for example, is based on an idea from Greek antiquity of using the interval between the second and third harmonics – a fifth – as a basis and then layering it twelve times.
Harmonic Series – Sound Sample
In the following video you will see and hear the overtone series of A3 (220 Hz). The video was recorded by Bodo Maass with our software Overtone Analyzer.
Chord of Harmonics
All partials of the overtone series sound simultaneously when singing and in instruments. Our brain combines these partial tone bundles into a single sound and assigns them to a sound source. The frequency spacing between the partials is perceived as the pitch, the volume distribution of the overtones as the timbre. Most singers are not aware of the fact that they always sing whole chords of harmonics. Our brain has an archaic knowledge of this chord. Obviously, it can identify partial chords as a single sound source even before birth, e. g. the mother voice.
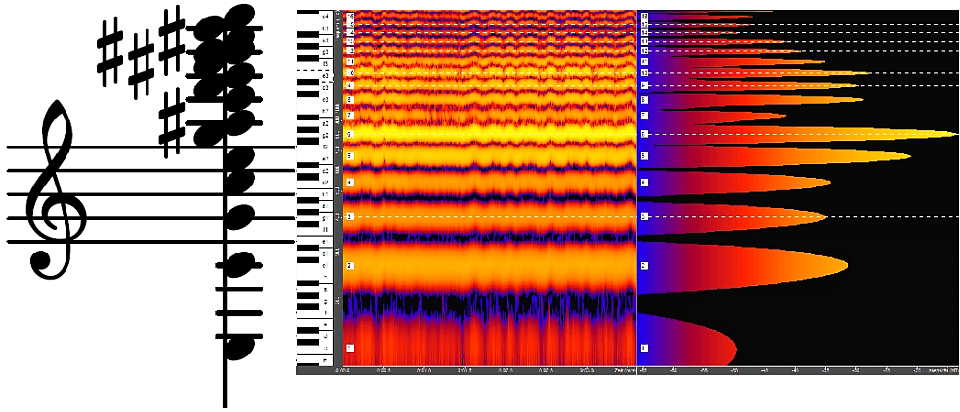
When singing tone C4, the entire series of overtones sounds as a chord.
Sound spectra and spectrograms can be used to visualize the relationship. Sound analysis software breaks down the sound into its individual frequencies and displays the volume levels by colours. The Overtone Analyzer, which was developed by Bodo Maass and myself, specializes in providing musicians with an easy-to-understand overview of sound contexts.
The sound spectrum (frequency spectrum) is one way of visualizing sound. The spectrum shows the volume distribution of the overtones in a sung vowel. Each peak corresponds to an overtone, the further right the peak, the louder the overtone. At the bottom is the fundamental. Upwards the frequency (pitch) increases, to the right the volume increases. (Recorded with Overtone Analyzer).
The spectrogram (also called sonagram) is a second way of displaying sounds. Here the volume is shown in colours, in the example the more red, the louder. Each transverse line corresponds to an overtone. At the bottom is the fundamental. Upwards the frequency (pitch) increases, from left to right runs the time. (Recorded with Overtone Analyzer).
Timbre
Such a chord of harmonics sounds like a single note, but it has a timbre. While a tone without overtones is colorless. A tone with overtones is called a sound (German: Klang) in physics. Musicians and physicists might mean different things with this word!
Different timbres are caused by different volumes of the harmonics (besides the noise components and transient response). The personal voice of a person is thus created by a typical volume distribution of the harmonics. If two people sing the same note, they differ only in the overtone volume. If you filter the overtones one by one, you will no longer recognize the individuals. The volume distribution contains a lot of information: Vowels, identification of the person, physical and mental state, age etc.
Spectrum of a sung note C3 with its harmonics and the typical volume distribution for the vowel æ.
Harmonic Series – Intervals
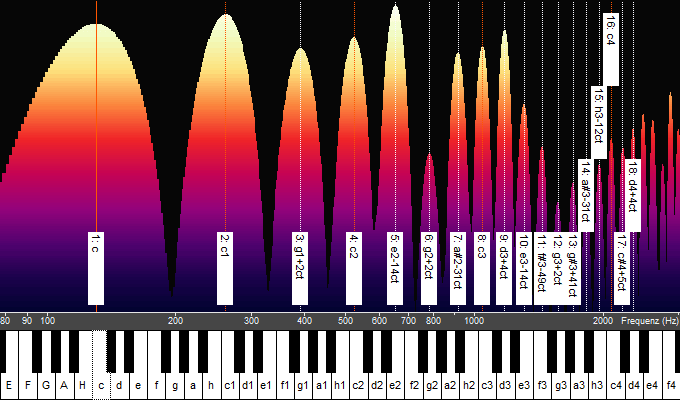
The interval sequence of the harmonic series is always the same. The intervals depend only on the position in the row. For example, the interval from the 2nd to the 3rd harmonic is always a fifth. Regardless of which tone you start with, the series results always in the same melody from the respective keynote. The intervals become increasingly narrower towards the top (while the frequency spacing remains the same, see below). All adjacent intervals are unique and occur only once in the series. Each interval repeats itself, once it has occurred, in the octaves above with new intermediate tones.
The overtone slider (picture) displays the intervals from harmonic to harmonic and from the fundamental to the harmonic. It is the keyboard of overtone singing so to speak. On one singing note, you can only perform intervals that occur in the slider, and usually only a part of them (cf. Ambitus of overtone singing). The interval to the fundamental tone determines the harmonic perception. For example, the 5th partial tone is perceived as major third. If you want to sing a quart in an overtone melody, you will find it between the 3rd and 4th harmonic and then you choose the fundamental accordingly.
Intervals of the harmonic series – the overtone slider.
Harmonic Series – Frequency Ratios
The frequencies of the harmonics are integer multiples of the fundamental frequency. This mathematical connection is called a “harmonic series”.
The frequency difference between two harmonics is always identical to the basic frequency, accordingly.
Calculation of the frequencies is therefore quite easy and clearly structured. Calculating the interval, however, is more complicated. While the frequency of an arbitrary harmonic is quickly calculated in the head, you better learn the intervals by heart (except you can calculate logarithms in your head…).
Calculating frequencies of the partials of C3 (130.8 Hz):
1st harmonic – 1-fold the frequency = 130.8 Hz 2nd harmonic – 2 times the frequency = 264.6 Hz, 3rd harmonic – 3 times the frequency = 392.4 Hz, … 11th harmonic – 11 times the frequency = 1,439 Hz etc.
All harmonics of C3 therefore have the same frequency spacing of 130.8 Hz.
The spacing of the partials of the fundamental note c (130.8 Hz) would then be – as you might have guessed – 130.8 Hz, i. e. always identical to the basic frequency.
Calculating frequencies of the partials of C3 (130.8 Hz):
1st harmonic – 1-fold the frequency = 130.8 Hz 2nd harmonic – 2 times the frequency = 264.6 Hz, 3rd harmonic – 3 times the frequency = 392.4 Hz, … 11th harmonic – 11 times the frequency = 1,439 Hz etc.
All harmonics of C3 therefore have the same frequency spacing of 130.8 Hz.
Musicians and Physicists
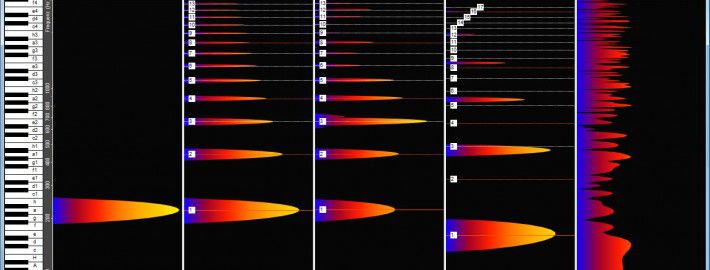
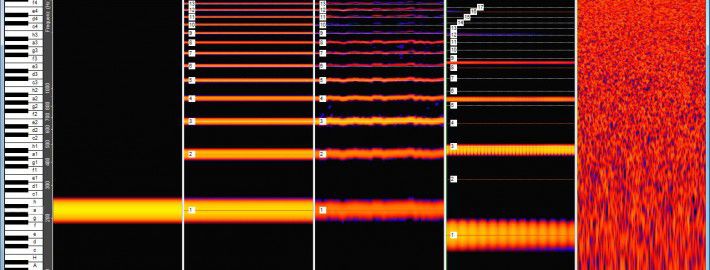
You can display the frequencies of the harmonic series linearly or logarithmically. Musicians prefer the logarithmic representation because the interval distances appear as we hear them. Physicists often represent the frequencies linearly. The following graphs illustrate the difference.
(1) Logarithmic frequency display for musicians: The intervals are important in the musical display. They are therefore presented as we hear them, namely linearly. Musicians only need frequency information for tuning. Advantages: Musicians understand the visualization intuitively, the intervals correspond to our listening.
(2) Linear frequency display for physicists: In the physical representation the frequencies are shown in such a way that frequency distances are immediately visible. Advantage: It is easier to calculate and you can see at a glance that all partials have the same frequency spacing, which is is identical to the basic frequency.
Converting Frequencies into Pitches
Our ear hears intervals as frequency ratios. A multiplication with the same number is heard as the same interval.
Example: 100 and 200 Hz have a frequency difference of 100 Hz. 200 Hz is double the frequency of 100 Hz, a frequency ratio of 2:1. A doubling (or halving) of a frequency is heard as an octave. Between 200 and 300 Hz there is again a 100 Hz difference. But 300 Hz are 3/2 times 200 Hz. This 100 Hz distance is heard as a fifth. So we do not hear equal distances, but equal ratios as equal intervals. 2:1 and 1:2 are octaves. 2:3 and 3:2 correspond to the fifth. 4:5, 5:4 are major thirds and so on. The corresponding intervals for the ratios can be found in the section Harmonic Series – Frequency Ratios.
The conversion from distance to ratio is done by the logarithm. Here is the formula to convert frequency differences into intervals.
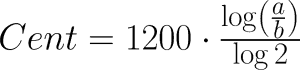
a = first frequency
b = second frequency
The results of this formula are cent values, that is 1/100 semitones. 100 cent is exactly one (equally tempered) semitone. 1200 cents are 12 semitones, that is one octave. 700 cents are 7 semitones, i.e. one fifth.
If values differ from even 100s, e.g. 702, this means that a tone differs by this cent amount from the standard equal temperament on the piano. 702, the pure fifth from the harmonic series, is thus 2 cents, 2 hundredths of a semitone higher than on the piano. The tones of the harmonic series all deviate from the equal temperament except for the octaves.
Overtones vs Harmonics
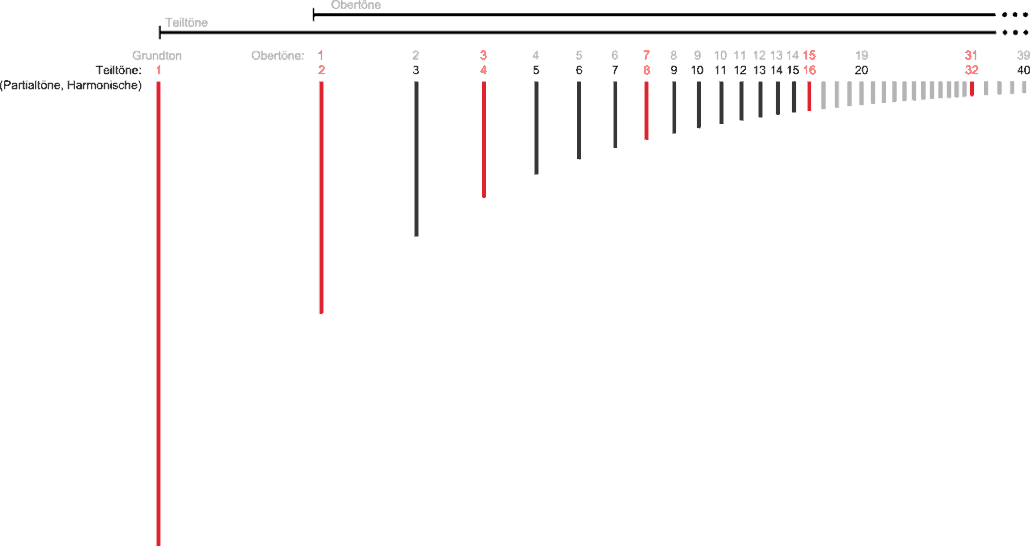
Overtones are numbered in two different ways. This is because some people count the fundamental, others do not. Overtones are actually only the tones above the fundamental. However, since the numbering including the fundamental has advantages, it is better to speak of harmonics (or partials), since the fundamental tone is also considered as a partial tone of the sound.
I prefer the numbering of partials (or harmonics, see below), thus including the fundamental.
- Partial tone numbering has the advantage that the frequency ratio results directly from the digit. The 14th partial tone has a 14-fold frequency of the fundamental tone, partial tone number 23 has a 23-fold frequency, etc.
- The frequency ratios of the intervals are also derived directly from the partial tone numbers. Example: The 3rd partial is the fifth in the 2nd octave. It has three times the basic frequency. The 2nd partial tone is the octave to the fundamental. The two adjacent partials 2 and 3 have a frequency ratio of 2:3 (upwards) or 3:2 (downwards) and sound as a fifth. Their doublings are fifths again. So the partial tone pairs 4/6, 8/12 etc. also form fifths with the same frequency ratio (since the fractions can be shortened to 2/3).
The illustration shows that the octaves are always even numbers in the case of partial tone (harmonics) numbering, whereas they are odd in the case of overtone numbering. This can be important for musicians: For example, the clarinet can only produce the odd partials by overblowing, i. e. no octaves. Even textbooks sometimes say that wrong. For overtone singers it has of course special meaning, because their music is notated with the partial tone numbers.
Natural Tone Series vs. Harmonic Series
The natural tone series (series played on brass instruments e. g.) has the same tonal structure as the harmonic series, but it is not the same. While the partials of the overtone series are pure sine waves, the tones of the natural tone series consist of individual harmonics.
| Natural Tone Series | Harmonic Series |
|---|---|
| Tone sequence that can be produced on wind instruments (tubes) by overblowing or changing the lip frequency. | Partials of a real sound. |
| Natural tones are real tones and have their own overtones. | Partial tones (harmonics) are pure tones and do not have overtones themselves. |
Examples: Harmonic series of F and E
With Overtone Analyzer software, you can instantly display overtone series of any tone, including tone name, frequency, and cent deviation from the tempered system, and you can listen to them right away. Download the free trial version.
Download the overtone series (1-24) as a MuseScore file (MuseScore freeware) and MusicXML file below and transpose and listen to it as needed. The cent deviations always remain the same for each harmonic position in the series. The notes in the files are tuned accordingly.
Harmonic series of F
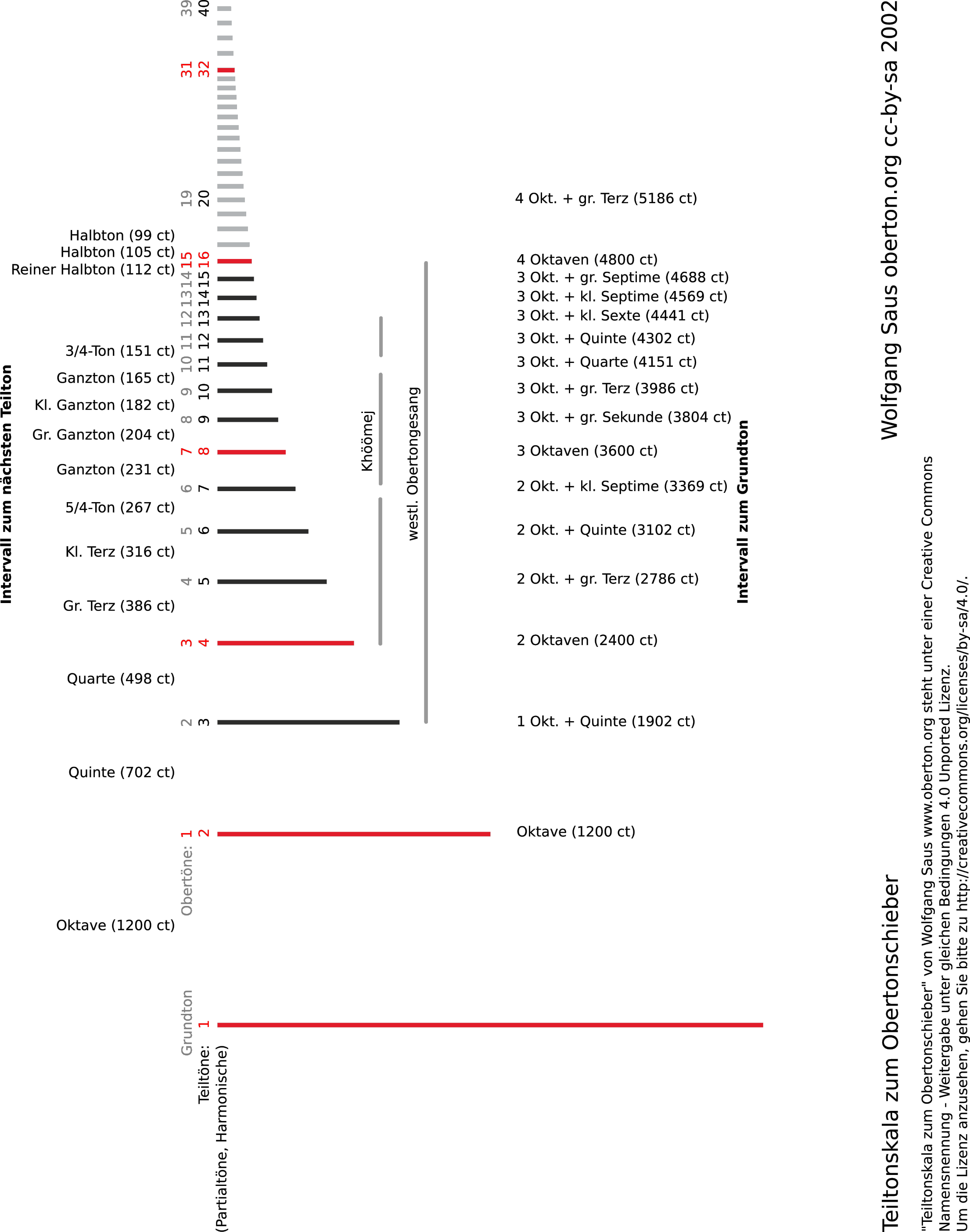
Table of Harmonics
Sometimes numbers are useful.
| Teilton-Nr. | Oberton-Nr. | Intervall zum Grundton | Cent zum Grundton | Intervall zum Teilton darunter | Cent zum Teilton darunter |
|---|---|---|---|---|---|
| 18 | 17 | 4 Oktaven + gr. Sekunde + 4ct | 5004 | kl. Sekunde -1ct | 99 |
| 17 | 16 | 4 Oktaven + kl. Sekunde +5ct | 4905 | kl. Sekunde +5ct | 105 |
| 16 | 15 | 4 Oktaven | 4800 | kl. Sekunde +12ct | 112 |
| 15 | 14 | 3 Oktaven + gr. Septime -12ct | 4688 | kl. Sekunde +19ct | 119 |
| 14 | 13 | 3 Oktaven + kl. Septime -31ct | 4569 | kl. Sekunde +28ct | 128 |
| 13 | 12 | 3 Oktaven + kl. Sexte +41ct | 4441 | kl. Sekunde +39ct | 139 |
| 12 | 11 | 3 Oktaven + Quinte +2ct | 4302 | 3/4-Ton | 151 |
| 11 | 10 | 3 Oktaven + überm. Quarte -49ct | 4151 | Gr. Sekunde +35ct | 165 |
| 10 | 9 | 3 Oktaven + gr. Terz -14ct | 3986 | Gr. Sekunde (Kl. Ganzton) +18ct | 182 |
| 9 | 8 | 3 Oktaven + gr. Sekunde +4ct | 3804 | Gr. Sekunde (Gr. Ganzton) +4ct | 204 |
| 8 | 7 | 3 Oktaven | 3600 | Gr. Sekunde +31ct | 231 |
| 7 | 6 | 2 Oktaven + kl. Septime -31ct | 3369 | 5/4-Ton | 267 |
| 6 | 5 | 2 Oktaven + Quinte +2ct | 3102 | Kl. Terz +16ct | 316 |
| 5 | 4 | 2 Oktaven + gr. Terz -14ct | 2786 | Gr. Terz -14ct | 386 |
| 4 | 3 | 2 Oktaven | 2400 | Quarte -2ct | 498 |
| 3 | 2 | Oktave + Quinte +2ct | 1902 | Quinte +2ct | 702 |
| 2 | 1 | Oktave | 1200 | Oktave | 1200 |
| 1 | Grundton | Prime | 0 | Prime | 0 |
- column: Numbering of partials including fundamental tone. This numbering is the more useful one.
- column: Numbering of overtones, the fundamental note is not counted.
- column: Interval to the fundamental tone with cents deviation to the nearest equally tempered tone.
- column: Interval to the keynote in cents (100-th semitone).
- column: Interval between the partials (to the lower ones) with cents deviation to the equal tempered interval.
- column: Interval between the partials in cents (100th semitone).
What are Overtones?
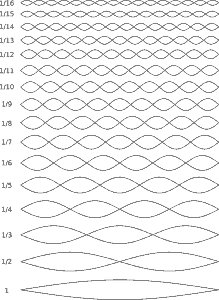
All vibrations are accompanied by faster oscillations.This is a universal behaviour of nature, whether it is sound or other vibrations.
Strings vibrate harmoniously. This means that in addition to the basic vibration, the string also vibrates in integral sections, i. e. over half the length, 1/3, 1/4, 1/5, etc. of the string length. These vibrations all occur simultaneously and superimpose each other to the total vibration. The partial oscillations look like the following figure.
The propagation of a wave in a string.
Stationary waves.
The wave is created in a string by the migration of pulses.
Glossary of Terms
Overtones, Partials, Harmonics….
Illustrations: Spectra (top) and spectrograms from left: 1) sinus tone, 2) synthetic sound (sawtooth tone), 3) natural sound (voice), 4) unharmonious sound (singing bowl), 5) noise (white noise).
Sine tones (Fig. 1. from the left) have no overtones, i. e. they are oscillations with only one frequency. The perceived pitch does not always correspond to that of a natural tone played at the same basic frequency. High sine tones often sound too low to us. Sine tones are a mathematical construct. Completely overtone free sounds are not existent, there is always a sound or noise component.
Sound (fig. 2. and 3. from left) in acoustics means a tone with overtones. In music, the term is usually used in a different way and can refer to the sound color, for example. Every real natural tone is a sound. Sine tones are only found in nature as an approximation.
Noises (fig. 5. from the left) are sound events that have such dense overtones or constantly changing overtone frequencies that we no longer perceive any pitch. But there are seamless transitions to sounds. Depending on the characteristic, one refers to either noises with a sound character or sounds with a noise component.
Partial tones (or simply partials) are the set of (sinusoidal) tones that make up a sound, including the fundamental tone. They are counted from the keynote (the one with the lowest frequency). There can be harmonic and unharmonic partials, even mixed. Harmonic partials oscillate with integer multiples of the basic frequency, inharmonic partials with non-integer ones.
Harmonics. Abbreviation for “harmonic partials”. Partial tones with integer multiples of the basic frequency are also called harmonics. For harmonics, the intervals always correspond to the natural overtone series. So harmonics are always also partial tones. Most melody instruments and the human voice have harmonious overtones.
Overtones are all partials above the fundamental. The numbering starts above the keynote, i. e. with the 2nd partial tone. Therefore, the numbering of the overtones is always 1 lower than that of the partials. There can be harmonic and unharmonic overtones, or both.
Unharmonic partials / overtones (Fig. 4. from left): Drums, bells, gongs, singing bowls or xylophones are examples of instruments with unharmonic partials / overtones. This means that the overtone frequencies are not (all) integer multiples of the lowest frequency. There also exist sounds that contain both harmonic and inharmonic overtones. It is often not possible to speak of a fundamental tone in the case of non-harmonic sounds, because the pitch that is heard is sometimes not that of the lowest frequency, such as the strike tone of a bell.
Bibliography & Sources
Itemizations
Literature Section Physics of the Harmonic Series
Harmonic overtones. By Qef [Public domain], via Wikimedia Commons
Als Physiker kannte ich dies alles bereits,
finde es aber echt gut erklärt! Kompliment!
Jetzt fehlt nur noch eine genauso gute Herleitung für
“Dur” + “Moll”.
WAS das ist und WIESO es so festgelegt ist…
Prima Artikel!
herzlichen Dank für den Abschnitt Musiker-Physiker. Das war genau wonach ich suchte!
Hallo Wolfgang,
nochmal bzgl. des Sinustons:
Hatte letztens Sabine und Astrid ( vom Workshop EBE)
den Overtone Analyzer gezeigt.Wir plagten uns zunächst auf
U einen auberen Sinuston zu erreichen, bis wir plötzlich merkten, dass
das auf einem dumpfen I viel einfacher geht.
Gibt’s das?
Liebe Grüße,
Beate
Super Infos, hilft mir wunderbar mit meiner Hausarbeit über Klangfarben. Ich hätte allerdings eine Frage, gibt es eine direkte Literatur bezüglich der Charakteristik von Klangfarben? Also eine Art Handbuch, welches mir zum Beispiel sagt, welcher Frequenzbereich welche Auswirkung auf den Klang hat. Ich lese auf verschiedenen Seiten immer wieder Dinge wie “Je weniger Obertöne erklingen, desto dumpfer, flacher und weicher ist die Klangfarbe”, allerdings finde ich nie Literaturangaben zu solchen Zitaten.
Beste Grüße und vielen Dank im Voraus.
Hallo Wolfgang,
Zu deinem Beitrag am 9.1.17
Meinst Du wirklich ein dunkelgefärbtes O für den Sinuston?
Wenn ich auf dem tiefen d ein hauchiges U singe ist beim Overtone Analyzer fast nix
anderes zu sehen (hören).Sobald ich nur Richtung O ‘denke’ kommt der 2.Teilton,also die Oktave hinzu.Um die Quinte (3.TT) in Vokaltechnik zu hören mach ich dann schon eher ein OA…
Aber vllt. liegt’s an der Sopranlage ?
Es macht auf jeden Fall Spass mit dem OTAnalyzer zu testen :)
Oft benutze ich statt des Begriffs Obertonreihe den Begriff Teiltonreihe, denn die Vorstellung von oben und unten basiert auf der Notenschrift und entspricht nicht der physikalischen Vorstellungswelt. Man kann auf diese Weise auch vom 4. Teilton sprechen und kommt damit sofort zur richtigen Zahl 4. Aber das soll keine Kritik sein, sondern lediglich das Aufzeigen einer anderen Möglichkeit. Bei dem Begriff Teiltonreihe hat sich auch die Frage erledigt, ob es eine Untertonreihe gibt. Zweifellos gibt es deratige tiefe Töne unter dem Bezugston, aber das würde ich nicht in unmittelbarer Beziehung zu den Teiltönen sehen.
Kurze Frage: wie klingt eigentlich ein Gesang, der kein Obertongesang ist? Ist nicht jeder Gesang ein Obertongesang?
sehr informative seite….
How does each harmonic get quieter in volume? Is the first overtone half as quiet? Is there a pattern it follows as well?
Thanks
Hi Pierce,
good question, thanks. Vocal harmonics directly above the vocal cords become quieter upward in a regular pattern. Depending on the singing technique, this is 12 decibels per octave for untrained voices, meaning the volume drops by half every octave, 6 decibels per octave for classical voices, and 3 decibels per octave for shouting or belting.
On the way to the mouth opening, the volumes are changed by resonances and form the timbres heard outside. (Actually, loudness is not the right term here, because loudness is a subjective sensation. The sound pressure is measured.)
Sehr schöne und hilfreiche Website. Klar verständlich und umfassend. Danke!