The Harmonic Series
The Musical Scale of Nature
Definition
The harmonic series is the chord of partials that vibrate simultaneously when a natural tone is played.
Inhalt
- 1 Harmonic Series – Sound Sample
- 2 Chord of Harmonics
- 3 Timbre
- 4 Harmonic Series – Intervals
- 5 Harmonic Series – Frequency Ratios
- 6 Musicians and Physicists
- 7 Converting Frequencies into Pitches
- 8 Overtones vs Harmonics
- 9 Natural Tone Series vs. Harmonic Series
- 10 Examples: Harmonic series of F and E
- 11 Table of Harmonics
- 12 What are Overtones?
- 13 Glossary of Terms
- 14 Bibliography & Resources
- 15 Picture Credits
- 16 Tell a Friend
The harmonic series is the basis of all pitch spaces, because it is the only natural scale. Overtones resonate as soon as a tone sounds. They all sound at the same time. So the harmonic series is actually a chord. The structure is always the same and corresponds to a mathematical harmonic series, hence the name series. You normally don’t hear the overtones. Because they all vibrate simultaneously as a chord, they appear to us like a single note.
The term overtone series refers to the harmonic partials (to distinguish between overtone, partial and harmonic, see below). There are also sounds with inharmonic overtones. The more inharmonic overtones a sound contains, the more it acquires the character of a noise.
Harmonic series of A2 110 Hz
Harmonic series of A2 110 Hz.
All sounds consist of overtone chords. Only sine waves have no overtones. One sound differs from the other mainly by the volume of the individual overtones (besides noise components and temporal sound changes). The harmonic series is not only the basis for music, it allows us to speak and sing, to recognize people by their voice, to locate sounds and to distinguish a piano from a flute.
It follows a universal oscillation principle of the universe and makes it audible and tangible for us. The tones deviate from our familiar equally tempered scale. Nevertheless, the equally tempered system, like all other pitch systems, is based on the harmonic series.
The reason for this is that we internally assemble tone sequences into small chords and then unconsciously compare them with the overtone series. Because we love similarities with the overtone series, we invented scales based on natural intervals. However, cultures have not always found the same intervals beautiful. Therefore there are over 3000 different pitch spaces in the world.
Our western system with 12 semitones per octave, for example, is based on an idea from ancient Greece: we use the interval between the second and third harmonics – the perfect fifth – as a basis and then layer it twelve times on top of each other.
Harmonic Series – Sound Sample
In the following video you see and hear the overtone series of A3 (220 Hz). The video was recorded by Bodo Maass with our software Overtone Analyzer.
Chord of Harmonics
When singing and in instruments, all partials of the overtone series sound simultaneously. Our brain combines these partial tones into a single note and assigns them to a single sound source. The frequency spacing between the partials is perceived as the pitch, the volume distribution of the overtones as the timbre. Most singers are not aware that they always sing whole chords of partials. Our brain has an archaic knowledge about this chord. It can apparently recognize partial chords as sounds of one sound source even before birth, e.g. the mother voice.
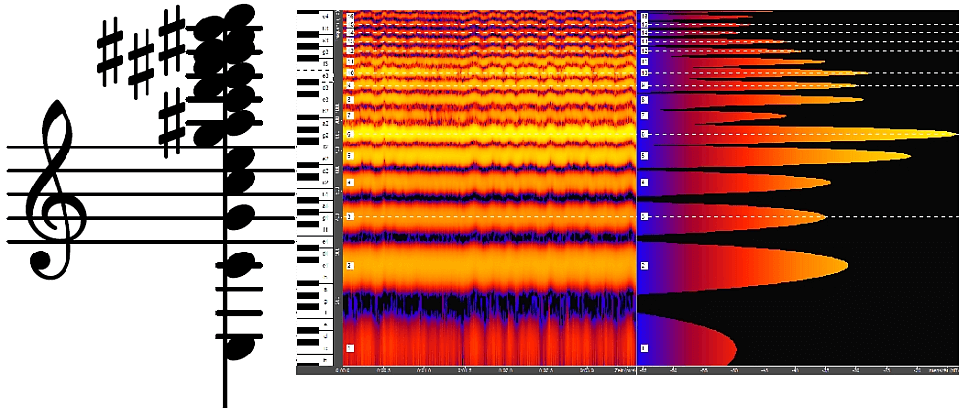
Harmonic series of C3 as a chord, with spectrum and spectrogram
When singing the note C3, the entire overtone series is heard as a chord.
Timbre
Such a chord of partials sounds like a single note, which has a timbre. While a note without overtones (sine wave) is colorless. A tone with overtones is called a sound in physics. Musicians and physicists may mean something different with this word!
Different timbres are created by different volumes of the overtones besides noise and attack characteristics. A person’s personal vocal sound is thus created by a distribution of the volume of the overtones that is individual for each person. If two people sing the same tone, then they differ only in the overtone volumes. If the overtones are filtered individually, the person is no longer recognizable. The volume distribution contains countless pieces of information: Vowels, identification of the person, physical and mental condition, age, etc.
Spectrum of a sung C3 with its overtones and the typical volume distribution for the vowel æ.
Sound spectra and spectrograms can be used to visualize that relationship. Sound analysis programs break down the sound into its individual frequencies and display the volumes graphically in color. Overtone Analyzer, developed by Bodo Maass and myself, is specialized in presenting sound concepts to musicians in a way that is easy to understand.
The sound spectrum / frequency spectrum is a possibility to visualize sound. The spectrum displays the volume distribution of the overtones of the sung vowel. Each peak corresponds to an overtone, the further to the right the peak, the louder is the overtone. At the bottom is the fundamental. Upwards the frequency, i.e. the pitch, rises, and to the right the volume increases. (Recorded with Overtone Analyzer).
The spectrogram (also called sonagram) is another form of visualization for sounds. The volume is shown here in colors. In the example more red means louder. Each horizontal line corresponds to an overtone. At the bottom we see the fundamental. The frequency, i.e. the pitch, increases upwards. Time runs from left to right. (Recorded with Overtone Analyzer).
Harmonic Series – Intervals
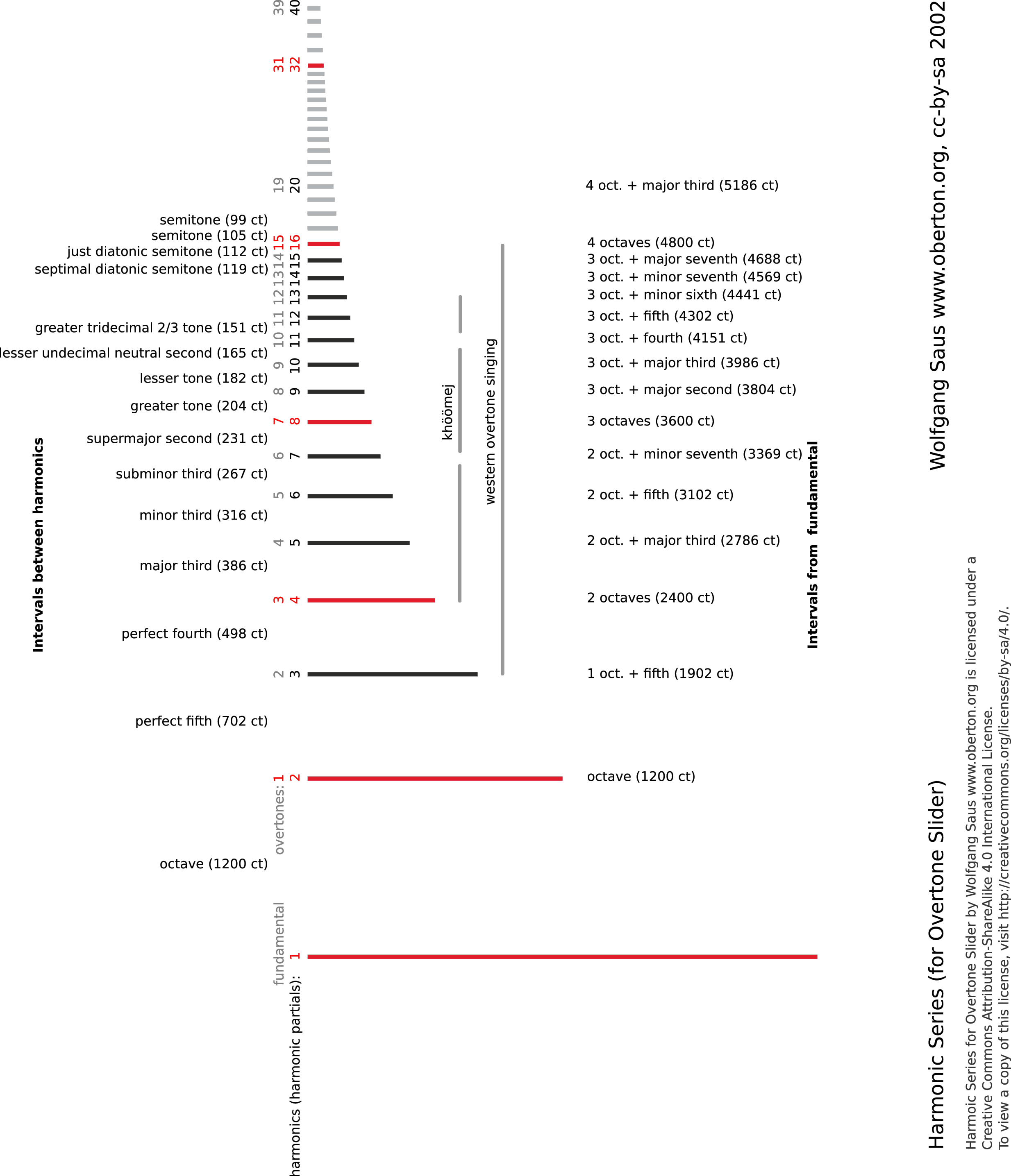
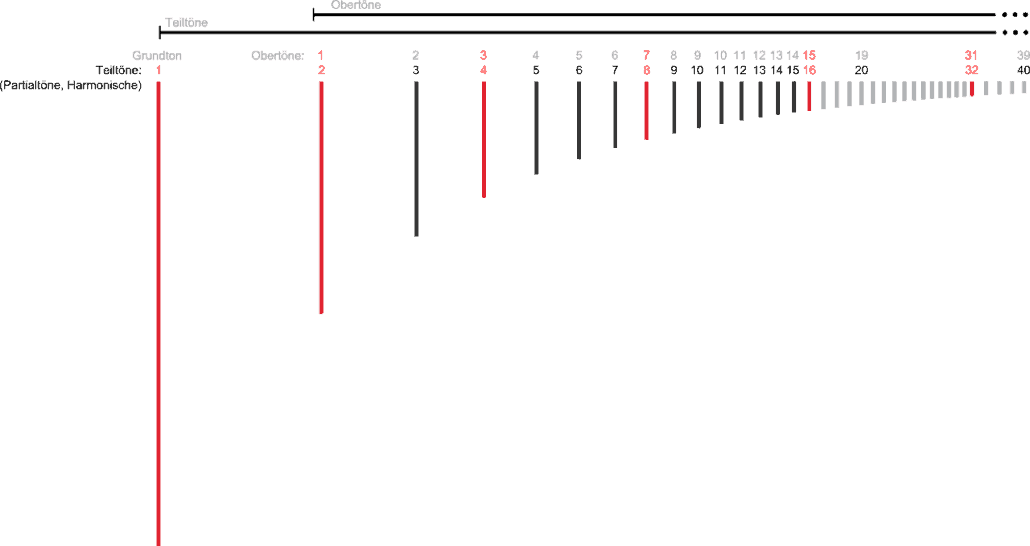
The interval sequence of the harmonic series is always the same. The intervals depend only on the position in the row. For example, the interval from the 2nd to the 3rd harmonic is always a fifth. Regardless of which tone you start with, the series results always in the same melody from the respective keynote. The intervals become increasingly narrower towards the top (while the frequency spacing remains the same, see below). All adjacent intervals are unique and occur only once in the series. Each interval repeats itself, once it has occurred, in the octaves above with new intermediate tones.
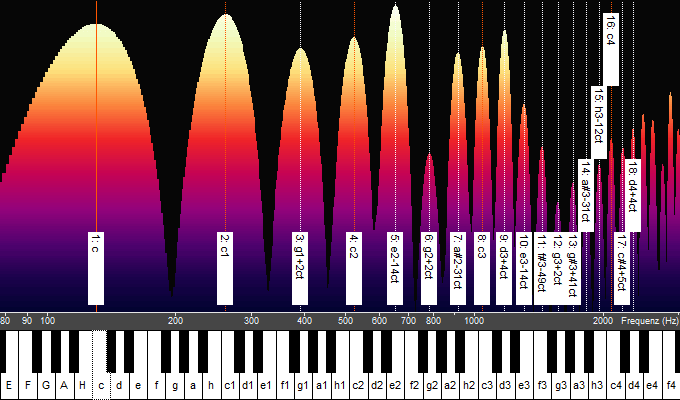
The overtone slider (picture) displays the intervals from harmonic to harmonic and from the fundamental to the harmonic. It is the keyboard of overtone singing so to speak. On one singing note, you can only perform intervals that occur in the slider, and usually only a part of them (cf. Ambitus of overtone singing). The interval to the fundamental tone determines the harmonic perception. For example, the 5th partial tone is perceived as major third. If you want to sing a quart in an overtone melody, you will find it between the 3rd and 4th harmonic and then you choose the fundamental accordingly.
Intervals of the harmonic series – the overtone slider.
Harmonic Series – Frequency Ratios
The frequencies of the partials are integer multiples of the fundamental frequency. This mathematical relationship is called a “harmonic series”.
This means that the frequency spacing between two partials is always identical to the fundamental frequency.
The frequencies can therefore be calculated very easily and displayed clearly. The calculation of intervals from the frequencies is more complex this way, however. While the frequency of any partial tone is quickly mental-calculated, you better learn the intervals by heart (unless you can calculate logarithms in mentally..).
Calculating frequencies of the partials of A2 (110 Hz):
1st harmonic – 1-fold the frequency = 110 Hz
2nd harmonic – 2 times the frequency = 220 Hz,
3rd harmonic – 3 times the frequency = 330 Hz,
…
11th harmonic – 11 times the frequency = 1210 Hz etc.
All harmonics of A2 therefore have the same frequency spacing of 110 Hz.
The pitch of the partials of the fundamental note c (130.8 Hz) would then be – as you might have guessed – 130.8 Hz, i. e. always identical to the basic frequency.
Calculating frequencies of the partials of C3 (130.8 Hz):
1st harmonic – 1-fold the frequency = 130.8 Hz
2nd harmonic – 2 times the frequency = 264.6 Hz,
3rd harmonic – 3 times the frequency = 392.4 Hz,
…
11th harmonic – 11 times the frequency = 1,439 Hz etc.
All harmonics of C3 therefore have the same frequency spacing of 130.8 Hz.
Musicians and Physicists
You can display the frequencies of the harmonic series linearly or logarithmically. Musicians prefer the logarithmic representation because the interval distances appear as we hear them. Physicists often represent the frequencies linearly. The following graphs illustrate the difference.
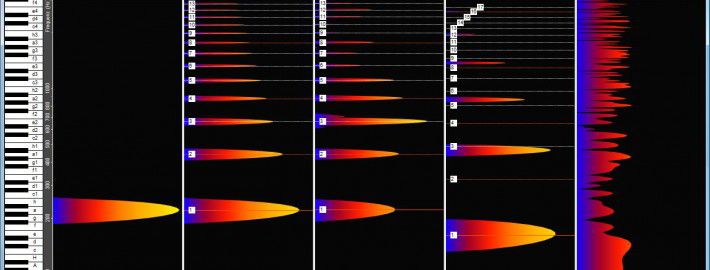
(1) Logarithmic frequency display for musicians: For musicians the intervals are important. They are therefore represented as we hear them. Musicians rarely need frequency information, mainly for tuning.
Advantages of this representation: musicians understand them intuitively, the interval distances correspond to our hearing. (Overtone Analyzer screenshot)
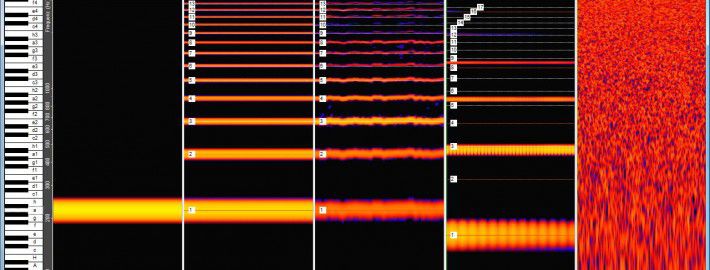
(2) Linear frequency display for physicists: In the physical representation the frequencies are shown in such a way that frequency distances are immediately visible.
Advantage: It is easier to calculate and you can see at a glance that all partials have the same frequency spacing, which is identical to the fundamental frequency. (Overtone Analyzer screenshot)
Converting Frequencies into Pitches
Our ear hears intervals as frequency ratios. A multiplication with the same number is heard as the same interval.
Example: 100 and 200 Hz have a frequency difference of 100 Hz. 200 Hz is double the frequency of 100 Hz, a frequency ratio of 2:1. A doubling (or halving) of a frequency is heard as an octave. Between 200 and 300 Hz there is again a 100 Hz difference. But 300 Hz are 3/2 times 200 Hz. This 100 Hz distance is heard as a fifth. So we do not hear equal distances, but equal ratios as equal intervals. 2:1 and 1:2 are octaves. 2:3 and 3:2 correspond to the fifth. 3:4, 4:3 are major thirds and so on. The corresponding intervals for the ratios can be found in the section Harmonic Series – Frequency Ratios.
The conversion from distance to ratio is done by the logarithm. Here is the formula to convert frequency differences into intervals.
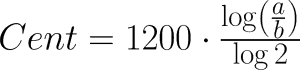
a = first frequency
b = second frequency
The results of this formula are cent values, that is 1/100 semitones. 100 cent is exactly one (equally tempered) semitone. 1200 cents are 12 semitones, that is one octave. 700 cents are 7 semitones, i.e. one fifth.
If values differ from even 100s, e.g. 702, this means that a tone differs by this cent amount from the standard equal temperament on the piano. 702, the pure fifth from the harmonic series, is thus 2 cents, 2 hundredths of a semitone higher than on the piano. The tones of the harmonic series all deviate from the equal temperament except for the octaves.
Overtones vs Harmonics
Overtones are numbered in two different ways. This is because some people count the fundamental, others do not. Overtones are actually only the tones above the fundamental. However, since the numbering including the fundamental has advantages, it is better to speak of harmonics (or partials), since the fundamental tone is also considered as a partial tone of the sound.
I prefer the numbering of partials (or harmonics, see below), thus including the fundamental.
- Partial tone numbering has the advantage that the frequency ratio results directly from the digit. The 14th partial tone has a 14-fold frequency of the fundamental tone, partial tone number 23 has a 23-fold frequency, etc.
- The frequency ratios of the intervals are also derived directly from the partial tone numbers. Example: The 3rd partial is the fifth in the 2nd octave. It has three times the basic frequency. The 2nd partial tone is the octave to the fundamental. The two adjacent partials 2 and 3 have a frequency ratio of 2:3 (upwards) or 3:2 (downwards) and sound as a fifth. Their doublings are fifths again. So the partial tone pairs 4/6, 8/12 etc. also form fifths with the same frequency ratio (since the fractions can be shortened to 2/3).
The illustration shows that the octaves are always even numbers in the case of partial tone (harmonics) numbering, whereas they are odd in the case of overtone numbering. This can be important for musicians: For example, the clarinet can only produce the odd partials by overblowing, i. e. no octaves. Even textbooks sometimes say that wrong. For overtone singers it has of course special meaning, because their music is notated with the partial tone numbers.
Natural Tone Series vs. Harmonic Series
The natural tone series (series played on brass instruments e. g.) has the same tonal structure as the harmonic series, but it is not the same. While the partials of the overtone series are pure sine waves, the tones of the natural tone series consist of individual harmonics.
| Natural Tone Series | Harmonic Series |
|---|---|
| Tone sequence that can be produced on wind instruments (tubes) by overblowing or changing the lip frequency. | Partials of a real sound. |
| Natural tones are real tones and have their own overtones. | Partial tones (harmonics) are pure tones and do not have overtones themselves. |
Examples: Harmonic series of F and E
With Overtone Analyzer software, you can instantly display overtone series of any tone, including tone name, frequency, and cent deviation from the tempered system, and you can listen to them right away. Download the free trial version.
Download the overtone series (1-24) as a MuseScore file (MuseScore is a freeware notation software) and MusicXML file below and transpose and listen to it as needed. The cent deviations remain the same for each harmonic position in the series. The notes in the files are already tuned accordingly.
Harmonic series of F
Table of Harmonics
Sometimes numbers are useful.
| Teilton-Nr. | Oberton-Nr. | Intervall zum Grundton | Cent zum Grundton | Intervall zum Teilton darunter | Cent zum Teilton darunter |
|---|---|---|---|---|---|
| 18 | 17 | 4 Oktaven + gr. Sekunde + 4ct | 5004 | kl. Sekunde -1ct | 99 |
| 17 | 16 | 4 Oktaven + kl. Sekunde +5ct | 4905 | kl. Sekunde +5ct | 105 |
| 16 | 15 | 4 Oktaven | 4800 | kl. Sekunde +12ct | 112 |
| 15 | 14 | 3 Oktaven + gr. Septime -12ct | 4688 | kl. Sekunde +19ct | 119 |
| 14 | 13 | 3 Oktaven + kl. Septime -31ct | 4569 | kl. Sekunde +28ct | 128 |
| 13 | 12 | 3 Oktaven + kl. Sexte +41ct | 4441 | kl. Sekunde +39ct | 139 |
| 12 | 11 | 3 Oktaven + Quinte +2ct | 4302 | 3/4-Ton | 151 |
| 11 | 10 | 3 Oktaven + überm. Quarte -49ct | 4151 | Gr. Sekunde +35ct | 165 |
| 10 | 9 | 3 Oktaven + gr. Terz -14ct | 3986 | Gr. Sekunde (Kl. Ganzton) +18ct | 182 |
| 9 | 8 | 3 Oktaven + gr. Sekunde +4ct | 3804 | Gr. Sekunde (Gr. Ganzton) +4ct | 204 |
| 8 | 7 | 3 Oktaven | 3600 | Gr. Sekunde +31ct | 231 |
| 7 | 6 | 2 Oktaven + kl. Septime -31ct | 3369 | 5/4-Ton | 267 |
| 6 | 5 | 2 Oktaven + Quinte +2ct | 3102 | Kl. Terz +16ct | 316 |
| 5 | 4 | 2 Oktaven + gr. Terz -14ct | 2786 | Gr. Terz -14ct | 386 |
| 4 | 3 | 2 Oktaven | 2400 | Quarte -2ct | 498 |
| 3 | 2 | Oktave + Quinte +2ct | 1902 | Quinte +2ct | 702 |
| 2 | 1 | Oktave | 1200 | Oktave | 1200 |
| 1 | Grundton | Prime | 0 | Prime | 0 |
- column: Numbering of partials including fundamental tone. This numbering is the more useful one.
- column: Numbering of overtones, the fundamental note is not counted.
- column: Interval to the fundamental tone with cents deviation to the nearest equally tempered tone.
- column: Interval to the keynote in cents (100-th semitone).
- column: Interval between the partials (to the lower ones) with cents deviation to the equal tempered interval.
- column: Interval between the partials in cents (100th semitone).
What are Overtones?
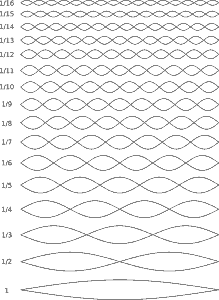
All vibrations are accompanied by faster oscillations.This is a universal behaviour of nature, whether it is sound or other vibrations.
Strings vibrate harmoniously. This means that in addition to the basic vibration, the string also vibrates in integral sections, i. e. over half the length, 1/3, 1/4, 1/5, etc. of the string length. These vibrations all occur simultaneously and superimpose each other to the total vibration. The partial oscillations look like the following figure.
The propagation of a wave in a string.
Ausbreitung einer Welle in einer Saite.
Stationary waves.
Stehende Wellen.
The wave is created in a string by the migration of pulses.
Entstehen der Welle in einer Saite durch Wanderung von Impulsen.
Glossary of Terms
Overtones, Partials, Harmonics….
Illustrations: Spectra (top) and spectrograms from left: 1) pure tone (sine wave), 2) synthetic sound (sawtooth wave), 3) harmonious natural sound (voice), 4) unharmonious natural sound (singing bowl), 5) noise (white noise). (Overtone Analyzer screenshot)
Sine tones (Fig. 1. from the left) have no overtones, i. e. they are oscillations with only one frequency. The perceived pitch does not always correspond to that of a natural tone played at the same basic frequency. High sine tones often sound too low to us. Sine tones are a mathematical construct. Completely overtone free sounds are not existent, there is always a sound or noise component.
Sound (fig. 2. and 3. from left) in acoustics means a tone with overtones. In music, the term is usually used in a different way and can refer to the sound color, for example. Every real natural tone is a sound. Sine tones are only found in nature as an approximation.
Noises (fig. 5. from the left) are sound events that have such dense overtones or constantly changing overtone frequencies that we no longer perceive any pitch. But there are seamless transitions to sounds. Depending on the characteristic, one refers to either noises with a sound character or sounds with a noise component.
Partial tones (or simply partials) are the set of (sinusoidal) tones that make up a sound, including the fundamental tone. They are counted from the keynote (the one with the lowest frequency). There can be harmonic and unharmonic partials, even mixed. Harmonic partials oscillate with integer multiples of the basic frequency, inharmonic partials with non-integer ones.
Harmonics. Abbreviation for “harmonic partials”. Partial tones with integer multiples of the basic frequency are also called harmonics. For harmonics, the intervals always correspond to the natural overtone series. So harmonics are always also partial tones. Most melody instruments and the human voice have harmonious overtones.
Overtones are all partials above the fundamental. The numbering starts above the keynote, i. e. with the 2nd partial tone. Therefore, the numbering of the overtones is always 1 lower than that of the partials. There can be harmonic and unharmonic overtones, or both.
Unharmonic partials / overtones (Fig. 4. from left): Drums, bells, gongs, singing bowls or xylophones are examples of instruments with unharmonic partials / overtones. This means that the overtone frequencies are not (all) integer multiples of the lowest frequency. There also exist sounds that contain both harmonic and inharmonic overtones. It is often not possible to speak of a fundamental tone in the case of non-harmonic sounds, because the pitch that is heard is sometimes not that of the lowest frequency, such as the strike tone of a bell.
Bibliography & Resources
Itemizations
Bibliography Section Physics of the Harmonic Series
Harmonische Obertöne. By Qef [Public domain], via Wikimedia Commons
Leave a Reply
Want to join the discussion?Feel free to contribute!